私大文系入試で最高難易度と呼び声の高い、早稲田大学商学部の数学の問題を解いていきます。
7回目の今回は2016年です。
第1問(1)

余りを求める問題です。
2016に近い2進数が2^11=2048なので、これを利用して合同式を使いまくります。その際、2048-2016=32なので、残った32もまた2進数なのでうまくできている問題だと言えます。
※計算ミスがあったので、訂正しました。
<筆者の解答>
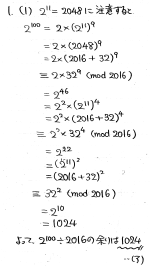
第1問(2)

3次方程式の有理数解についての問題です。
考える方程式は全部整数係数なので、有理数解の候補は、(3の約数)/(2の約数)の形に限られます。よって、1以上でこれに該当する1, 3/2, 3が解になる条件をそれぞれ考えればよいでしょう。
<筆者の解答>

第1問(3)

正n角形をいくつ作れるかを調べる問題です。
Pの頂点で正n角形を作ろうとすると、nは2016の約数に限ります。あとは、各nに対して正n角形がいくつ作れるかを考えてあげればよいでしょう。n=1,2がNGなことには注意しましょう。
<筆者の解答>

第1問(4)

三角関数のΣの計算問題です。
問題文のままの状態だとシグマがうまく計算できないので、外側にあるsin(π/2016)をΣの中に入れてどうにかしたいです。
その状態で和積の公式を使うとcosの差の形に分解できます。そしてcosの中身の番号がちょうど1ズレています。となると、思いつくのは「間が次々に相殺されて、最初と最後だけが生き残る」Σ計算です。その形になるように調整してあげると、最後に残るΣはΣcos(k-1)π/1008のみになります。
あとはこれをどう計算するかですが、このΣは、cosxのx=πでの対称性を使ってあげれば0だとわかります(別解のように、複素平面を使っても確かめられます)。
<筆者の解答>

第2問

線分の通過領域の面積を求める問題です。
(1) bをaで表して平方完成してあげればよいです。
(2) 各条件からα,βを1文字に統一して範囲を求めておくと、線分P1P2の通過領域を考えることに帰着します。
まずは「直線」P1P2の通過領域を求めて、それをy=x^2で切り取ってあげれば、「線分」P1P2の通過領域になります。通過領域は、答案では順像法で求めています。
あとは、この領域の面積を積分で計算してお終いです。
<筆者の解答>


第3問

対称な点を考える問題です。
まずは、△A0B0C0の概形を調べるのが第1です。余弦定理を使うと、実は∠A0=60°だと分かります。
私は、これを利用してA0を原点とする座標軸を取ることを考えました。(A0との距離をひたすら答えさせる設問なので、この点を原点にしておけば好都合です)
(1)線分A0A1と線分B0C0とが垂直で、A0A1の中点がB0C0上にある、という2条件からA1の座標が求まります。
座標軸を取らずとも、三角比だけで計算することも可能かと思います。
(2)A1, B1, C1, A2を実際に図に書いてみると、△A0A1A2がA1を頂角とする2等辺三角形になっていることが分かるので、あとは頂角の大きさが分かれば余弦定理で底辺A0A2を計算することができます。
頂角の大きさは、図から求めることができ、綺麗な角度になります。
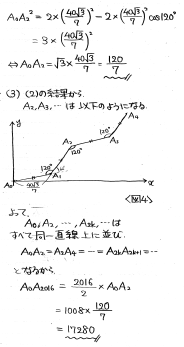
(3) (2)の知見を使ってA3, A4・・・を描いていくと、A0, A2, A4・・・が全て一直線上にあって、なおかつA0A2=A2A4=A4A6=・・・となることが分かります。
<筆者の解答>