このシリーズでは、東京大学の後期の数学の問題を解いていきます。
2回目の今回は2006年です。
第1問

パラメータ表示された曲線の概形を調べる問題です。誘導が丁寧なので、うまく乗っていきましょう。
(1) dx/dt, dy/dtがそれぞれ調べられ、dy/dx=(dy/dt)/(dx/dt)で求まります。
(2) (1)の結果から方程式を解くだけです。
(3) X,Yの式に元のCの式を代入することで、X,Yがtだけの式で書けますので、tを消去すればよいでしょう。このX,Yの関係式で書かれる曲線をC'とします。
(4)C'は(3)の結果から放物線となります。ところで、X,Yの定義式をよく見ると、(X,Y)=(回転行列)×(x,y)の形になっていることに気づきます。cosα=2/√5, sinα=1/√5とすると、C'は「Cを、原点の周りに反時計回りに+α回転した図形」であることがわかります。逆に言えば、「C'を、原点の周りに時計回りに+α回転した図形」がCだと分かります。
要するに、Cは軸が斜めになった放物線だということです。
あとは(2)までで調べた情報を生かしていきます。
(1)ではt=-1を除いていましたが、逆に言うとt=-1ではdy/dxは発散します。つまり、t=-1に相当する点BでのCの接線はy軸平行になります。(2)に登場したAを、原点の周りに+α回転すると、C'の頂点となります。つまり、AはCの頂点だった、というわけです。
ここまで情報が揃えば、Cの概形を描けるでしょう。
<筆者の解答>


第2問

回転体の体積に関する問題です。
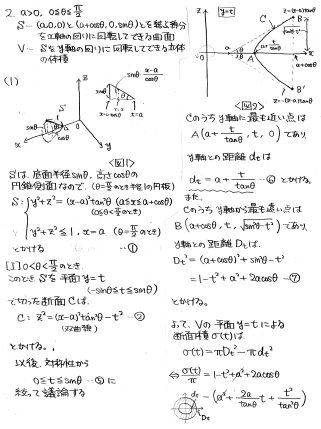
(1) Sは、基本的には底面半径sinθ, 高さcosθの円錐の側面になりますので、方程式を作ることができます(円柱側面にならないθ=0, π/2の場合は例外として個別に処理します)。
このSを平面y=tで切った断面をy軸の周りに回転したものが、Vのy=tによる断面になりますので、その断面積を調べてtで積分する、というのが全体に流れになります。
Sの断面は双曲線となり、回転体の断面積は、Sの断面のうちy軸に最も近い点との距離、最も遠い点との距離を調べれば事足ります。
例外処理したθ=0, π/2の場合も、最終的には0<θ<π/2の場合の式に合流させることができます。
(2) Vをθで微分すればよいのですが、増減表を書く時の符号に注意しましょう。
<筆者の解答>


第3問

Σ公式に関する問題です。
(1)Σ公式の導出過程をそのままなぞりつつ、帰納法で証明すればよいでしょう。Sm(n)を調べたいときは、Σ(k+1)^(m+1) - Σk^(m+1) を調べればよいんでした。
(2) 整数の絡んだ恒等式の証明では、
「F(n)=G(n)が恒等式⇔F(0)=G(0)が成立し、かつF(n+1)-F(n)=G(n+1)-G(n)が恒等式である」
という方法を使うのが定石です。今回の場合は、n=0での成立は自明なので、後者が恒等式であることの証明に全力を注ぐことになります。
与式の両辺を番号をずらして引き算してできる多項式の係数を比較してあげるとよいでしょう。
(3) (2)と基本的な方針は全く同じです。与式の左辺は偶数次だけで構成されていますが、右辺を計算すると奇数次も混じってしまいます。奇数次の項が消えるためにはcが特定の値でないといけません。
(4) (2), (3)の結果を使って帰納法で証明します。具体的には(2)の恒等式をxで微分したものを考えます。
<筆者の解答>



