このシリーズでは、山梨大学医学部後期の数学の問題を解いていきます。
9回目の今回は2014年です。
第1問(1)

定点を通る直線に関する、三角形の成立条件を考える問題です。
アについてはaの恒等式と見なしてx,yの連立方程式を解けばよいですね。
イについては、三角形ができない例としてy=xやx軸とlaが平行になる2パターンはすぐに分かるかと思いますが、「3直線が1点で交わる」を意外と見落としやすいので注意です。
<筆者の解答>
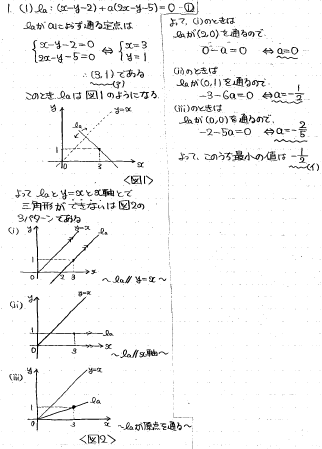
第1問(2)

直線に対する対称移動をあらわす行列を調べる問題です。
ウについてはCD⊥lとCDの中点がl上にあるという2条件を使って調べていき、その結果からMを構築していきます。
<筆者の解答>

第1問(3)

回転体の体積を求める問題です。
定石通りの積分計算で事足ります。
<筆者の解答>

第1問(4)
![]()
多項式の割り算に関する問題です。使う方法は勿論因数定理です。
余りは3次以下なのでax^3+bx^2+cx+dと置くことができますが、問題はx^4+x^3+x^2+x+1=0の解がどうなるかです。
この方程式はz^5=1とできるので、解は「1の1以外の5乗根」ということになります。その1つをαとすると、α^2, α^3, α^4もすべて方程式の解になるわけです。
こうしてx=α, α^2, α^3, α^4を全て代入すると、a~dの4つの方程式ができます。その際にα^5=1を利用することで指数を小さくできることに注意です。
この4つの方程式を直接解くのはかなりしんどいですが、実はa~dはすぐに見つかります。α^4+α^3+α^2+α+1=0と見比べればa=b=c=d=-1とすれば辻褄が合います。
4つの連立方程式は全部1次独立になっている(はず。確かめてはいませんが)ので、a~dはこの1つだけになります。
※1次独立でないとき、ある1本の方程式を他の方程式から作れてしまうことになるので、実質的に方程式の個数が減ってしまい、a~dが1通りとは限らなくなります。
<筆者の解答>


第1問(5)

極限の計算問題です。これは思いつかないと詰まってしまう難問ですね。かれこれ30分近く頭を捻ってようやく答えにたどり着きました・・・
見た目からして指数の中にさらに指数が入っていてヤバそうな気配を醸し出しています。
anの一般項は、1+c^(2^k)をk=1,・・・,n-1まで代入して積を取ったものになっています。1+c^(2^k)は1よりも少し大きい値で、kを大きくしていくとどんどん小さくなって1に近づいていきます。
つまり、1よりほんのちょっと大きい数を、小さくしつ次々とつかけていくというのがanなわけで、n→∞では1^∞の不定形になるというわけです。このタイプはネイピア数に帰着させることが多いのですが、今回はそれが使えない形なので悩みどころです。
対数を取って和に置き換えれば区分求積法!ともいかないため、最初は本当に詰んでしまってました。
ここは発想を切り替えて「そもそもanをもっと簡単な式で書けないか?」と考えてみることにしました。
a2,a3,a4辺りまで積を展開してみると規則性に気が付きます。anは実は公比c^2の等比数列の和の形になるのです(帰納法で証明できます)。
これに気が付けばanを単純な形に書き直せるので、極限計算も容易にできるようになります。
<筆者の解答>

第2問

確率の問題で、テニスのような「デュース」の概念を導入した点取りゲームが題材となっています。以後、分かりやすさのため、同点になっている状況を「デュース」と表現することにします。
(1)まず試合終了する状況としては以下の3パターンに分かれます。
1. デュースの末に第2mゲーム目で決着する(m=2,3,・・・,n)
2. 第2nゲーム目もデュースのまま終了する
3. どちらか一方がストレート勝ちする
デュースが発生する状況は、2k-1ゲーム目と2kゲーム目で得点者が異なる時です。それを繰り返した末に、最後の2m-1ゲーム目と2mゲーム目で一方が2連続で得点すればデュースが断ち切られて試合が終わる、というわけです。なので、決着するゲーム数は、ストレート勝ちである3を除けば必ず偶数になります。
そのことに着目して、確率を計算していきましょう。
(2)定義通りに期待値を計算していきますが、途中で等差数列×等比数列のΣ計算が要求されます。これは公比をかけて辺々引き算するというのが定番解法ですが、答案ではより楽に計算できるように微分を使って導出しています。
こうしてenがp,q,nの式で書けて、n→∞の極限も容易に計算できます。そして最後にp=q=1/2とすればフィニッシュです。
(※ストレート勝ちするパターンを後の方になって忘れていたことに気付いたので、その分の確率がとってつけた感じの表記になっちゃってます。。。)
enの極限をpに関する関数としてグラフにプロットすると下のようになります。

やはりというか、pが1/2に近いほど(お互いの実力が拮抗してるほど)ゲーム数の期待値は多くなる傾向がよく分かります。
テニスのグランドスラムの試合とかだとかなりの長丁場な試合になる、という経験からも明らかですね。
<筆者の解答>


第3問

行列に関する問題です。
(1)ケーリーハミルトンの定理から即座に示せます。
(2) (1)の結果を使うことで、x1,x2,y1,y2,zの方程式が2本求まります。
解があるかないかを問われているので、どっちの方針で攻めるか迷いどころです。そこそこ複雑な式であることもあり、「ないことを証明する」はちょっと機微そうなので、「解を1個でも見つける」方針で行くのが結果論正解です。
2本の式の内の1つは、x1=y1=1とするとピタゴラスの定理の形にできます。そこから連想すると、解が見つかると思います。
この手の「存在するか?」という問われ方だと、大体の場合「存在しない」が答えなことが多いです(反語ですし)が、今回は「存在する」だったので結構珍しいんじゃないでしょうかね。
<筆者の解答>

第4問

領域図示と面積の問題です。
(1)f(x)を微分することで極値を持つxが分かり、それをa≦x≦2aに代入することでbの不等式が出来上がります。両端の関数の形状を調べて図示していきます。
(2)S(t)は積分の形で求まりますが、今回は「S(t)が最大になるときのtの値」だけ求めればいい(つまりS(t)の最大値そのものは調べなくていい)ので、積分の状態からいきなり微分して増減調査に入ったほうが楽です。
<筆者の解答>

