このシリーズでは、日本医科大学の数学の問題を解いていきます。
11回目の今回は2012年です。
(問題文を提供して下さったせがわさん、ありがとうございます。)
第1問(1)

放物線上の2点の内分点が原点になる条件を考える問題です。
まずはP,Qのx座標をp,qとして、PQの式の一般形を先に作ってしまうとよいです。
(a) (OP+OQ)/2=0からp,qを求めていきます。
(b)OP/3+2OQ/3=0からp,qを求めていきます。
(c) 1/6公式を使うと効率よく解ける積分問題です。
<筆者の解答>

第1問(2)

シグマの計算問題です。
(a)~(c)すべてに共通して、まずはkを固定してjについて和を取って、その後にkについて和を取る形になります。
<筆者の解答>

第1問(3)

3次方程式の解に関する問題です。
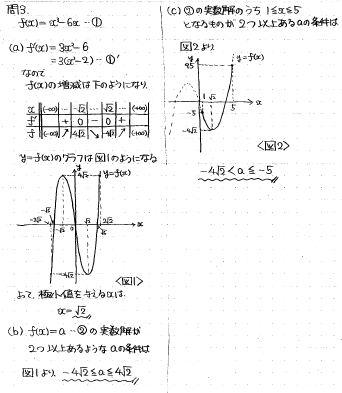
(a) f'(x)を計算してあげればよいです。(b)以降を見越してy=f(x)のグラフを描いておくとよいです。
(b) y=f(x)とy=aが2点以上で交わるようにaの配置を考えてあげます。
(c) こちらはy=f(x)のグラフを1≦x≦5の部分に限定して同じことをします。
<筆者の解答>
第2問

三角関数のΣの計算問題です。
(1)一般的にr, θkの式を求めてしまいましょう。AkAk+1を計算していくと(-sin〇, cos〇)という形が最終的に出て来ますが、三角関数の中身を〇+π/2に変えてあげると、x成分がcosに、y成分がsinに符号含めて変えることができます。
(2)問題文の指示に従って、計算あるのみです。
(3)実質sin2kαのΣ計算になるので、(2)の結果でαを2αに置き換えてあげればOKです。
(4)こちらもシグマの中身を展開すると、実質(3)に加えてcos2kαのΣ計算の結果があればよいことになります。極限を取る前の和がnの式で表現できるので、あとは不等式評価によるはさみうちを絡めつつ、極限計算をしていきます。
<筆者の解答>



第3問

点の動く範囲の体積を計算する問題で、これは難問ですね。
(1)K1の中心をA, K2の中心をB、長さ2以下のベクトルをr1, r2とすると、
K1に含まれる点PはOP=OA+r1、K2に含まれる点QはOQ=OB+r2と書くことができます。
このことに注意すると、OX=r1+r2となります。よって、長さが2以下になる2つの任意のベクトルを足して出来る点全体が、Xの動く領域、ということになります。
2つのベクトルを一度に考えると考えにくいので、「r1を固定してr2を動かす⇒r1の向きを固定して長さを0~2で動かす⇒r1の向きを自由にする」の段取りでXの動く領域を明らかにしていきます。
結果、Xは「原点中心の半径4の球の表面と内部」を隈なく動くことが分かります。
(2)問題文の「」の条件が分かりにくいので、分かりやすく言い換えていきます。
(1)の考え方を援用すると、まずは「OY=OA+r3となる、長さ2以下のベクトルr3が存在する」と言い換えられます。
さらに(1)の結果も生かしつつ言い換えていくと、
「OX+OR=3OA+3r3となる、長さ2以下のベクトルr3が存在する」
↓
「|OX+OR-3OA|=3|r3|≦6が、(1)を満たす全てのXについて成立する」
とまで言い換えられます。
また、OX'=3OA-OXと置き換えてあげると、X'は(1)の結果から「中心(3,0,0), 半径4の球の表面と内部を隈なく動く」ことが分かるので、
結局、問題文の「」は、
「中心(3,0,0), 半径4の球の表面と内部にある任意の点X'について|X'R|≦6が成り立つ」
とまで言い換えることができます。
ここまで言い換えてあげれば、Rは「中心(3,0,0), 半径2の球の表面と内部を隈なく動く」ことが分かります。
(3) 正直この小問については自信があまりありませんが、一応考え方を書いておきます。
(2)で「YがK1に含まれる」を「YがK2に含まれる」に書き換えてあげたときのRの動く領域は(2)と全く同じように計算でき、「中心(-3,0,0), 半径2の球の表面と内部」とわかります。
(2)の結果とこの領域の和集合が、(3)におけるRの動く領域と考えられ、この両者は体積が等しく共通部分がないので、(2)の結果をそのまま2倍すればよい、となると思います。
<筆者の解答>

