私立最難関の一角、慶應義塾大学の理工学部の問題を取り上げます。
今回から2000年以前の問題を解いていきます。
第1問

足し算での表現の仕方を数える問題です。
(1)アは実際に書き出せばよく、イについては「ちょうど4個の自然数の和で7を表す方法」を調べればよいでしょう。
(2) nの偶奇の場合分けに注意できれば、難しくないです。
(3)「nをちょうどk個の自然数で表現する方法」が何通りあるかを考えていきます。
これには少し発想力が要りますが、1をk個並べて、残りのn-kをk個以内に分解して足せばよいですね。
(4) (3)の結果でk=3として、nを6n, 6n-3にそれぞれ置き換えたものを考えればp3(6n)の漸化式を作ることができますので、それを解いていきます。
<筆者の解答>


第2問

確率の問題です。
(1) 誘導に従って定義通りに計算していけばよいです。
(2) (1)と同じように考えればよいです。i番目のコインがk回目に初めて表になる確率を考えましょう。
(3)この大問の一番の山場です。
rk-1 - rkを計算すると2種類のΣの積の形になるので、それを一まとめにしてΣの中身を整理していきます。すると因数にpi-pjが出てくるので、i=jの場合はすべて0になって消えます。残りはi>jの場合とi<jの場合の和になり、後者は対称性からiとjの文字を入れ替えることができます。
こうしてi>jの場合だけの和にできます。
(4) (3)が計算しきれなくても解くことができる親切設計です。
nもmも公比1-piの等比数列の和の形になっているので、公比の中で一番大きいもので割って考えればよいでしょう。
<筆者の解答>


第3問

分数関数の特定と、それに関する面積の問題です。
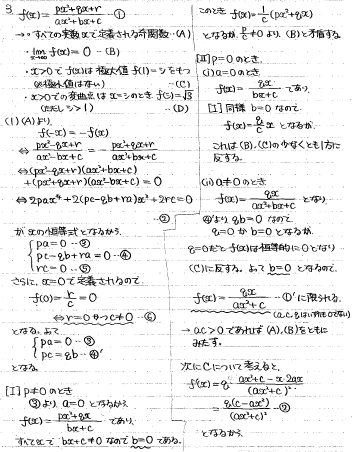
(1)(2)奇関数という条件から関係式をつくることができ、特にr=0とpa=0が得られます。pa=0は「pとaの少なくとも一方が0」と言い換えられるので、場合分けして残りの条件と合致するかを調べていきます。
(3)2曲線の交点を調べて積分していけばよいですが、かなり計算が大変です。特に工夫する余地もないので、力づくで計算していくほかないです。
面積の増減は、logの中身だけ微分して調べるとよいです。
<筆者の解答>


第4問

空間上での点の存在領域と、その面積を計算する問題です。
(1)一旦Aを固定してあげると、BはAを中心とした半径3の球面を描きます。この状態でAを動かした時の、この球面の通過領域を考えればよいです。
(2) (1)と同様に、BC=√11, CP=√11となるようなBの存在範囲を調べると、それと(1)の共通部分が、考えるべきBの存在範囲になります。
x軸を回転軸にした回転体になることに注意して積分しましょう。
<筆者の解答>

第5問

関数の値域に関する問題です。
(1)これは典型問題ですね。x^2+1/x^2は、(x+1/x)^2 -2と変形できます。
(2) v(y)は、caを2次の係数とする2次関数なので、caの符号による場合分けが発生します。
このとき、上記の場合分けによらずv(2)もv(-2)が2乗の形、つまり0以上になることがポイントです。他に注目するべき点は、2次関数の頂点の値です。
<筆者の解答>

