2023年も大学入試のシーズンがやってきました。 今回は、早稲田大学の商学部に挑戦します。
<概略> (カッコ内は解くのにかかった時間)
1(1): 面積の不等式評価 (20分)
1(2): 三角形の内接円 (10分)
1(4): 格子点に関する確率 (50分)
2: 球に内接する四面体(20分)
3: 整数問題(30分)
計155分
<体感難易度>
1(2)<1(1)<2<1(3)<3<1(4)
昨年の異常すぎる高難易度に比べれば、大幅に落ち着いた印象です。とはいえ、検討が面倒なイヤらしい問題は相変わらず健在です。
<個別解説>
第1問

小問集合です(といっても1問1問がかなり重く実質大問4つという感じです)
(1)面積の不等式評価の問題です。
S(n)をn-1個の台形に分割して、それぞれの面積を計算しΣをとればよいです。途中等差数列×等比数列のΣが登場しますが、こちらは公比をかけて差を取るというのが定石ですね。
S(n)を2^nで割ると、実質「nの1次関数+ 公比1/2の指数関数」≧2023の形となります。
nが十分大きい所では、前半の1次関数に比べて後半の指数関数はゴミのような値になりますので、左辺の値はほとんど前半の1次関数で決まると言ってよいです。
この考えのもとでnの当たりを付けてあげればよいでしょう。
(2)三角形の内接円に関する問題です。
外接円が登場していてsinの値が与えられているので、正弦定理を使うことで各辺の長さが計算できます。
こうすれば三角形の面積と周長が求まるので、それを利用すれば内接円半径が計算できます
(ぶっちゃけ、m,nは自然数である必要ないですよね。。。)
[訂正]
実はsinの関係式と正弦定理の結果から、△ABCはC=90°の直角三角形だと分かります。ということはsinC=1になるので、そこから(m,n)の値を特定することができました。
なので、m,nが残ったままでは不十分で、その特定した値をちゃんと代入するまでやらないといけませんでした。
nが最小になるものを知りたいので、n=1,2,3・・・と次数が小さい順に力づくで調べていった方が速いかと思います。(どこまで調べればいいかが初見では分からないので、不安にはなるでしょうけど)
積分の処理については、|x|^mが偶関数であることに注意すると、偶関数・奇関数の性質から見通しよく計算できます。積分区間を0以上に限定すれば絶対値も外れてくれます。
言うまでもないですが、(iii)についてはmに関する恒等式になる条件を調べます。
(4)格子点に関する確率 の問題です。
r1~r3は「3で割った余り」なので、値は0,1,2のどれかになります。ということは、(*)で決まる点は全部で3^3=27通り存在することになります。
最初、私はA1~A3の全ての座標を文字でおいて、△A1A2A3が正三角形になる条件を内積等で調べるという解法を取ろうとしたのですが、非常に調べにくいことが分かったので断念しました。
(50分という時間がかかってしまったのも、この初手の解法選択のしくじりによるものです・・・答案に上げた解法では正味20分程度です)
さて、上記の27点全てを図に起こしてみると、これらの点は立方体状に存在する格子点になっていることが分かり、この図から「正三角形を作るなら、立方体の頂点を考えればよさそうだ」と分かります。
ここで、27通りの点の決められ方は、rが0,1,2になる確率が等確率なので、結局すべて同様に確からしいことになります。なので、確率計算の際は、実質「正三角形になるようなA1~A3の選び方」の場合の数を調べればよいことになります。
各立方体について正三角形は8通りでき、A1~A3の順番を考慮するとこれに3!をかける必要があります。
そして、立方体は、小さいものが8個、大きいものが1個の合計9個作れるので、これで場合の数の調査が完了ですね。
[訂正]
実は上記以外に、「立方体の頂点にならない格子点を使った三角形が作れる」という指摘を頂きました。これは初見では完全に抜け落ちておりました。
なので、このパターンの場合の数を追加し、確率を再計算しました。
<筆者の回答>
(1)
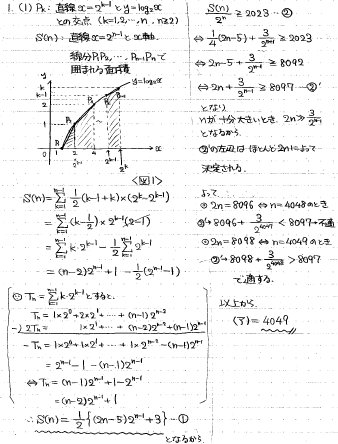
(2)

(3)


(4)

(4)の追加です

第2問

球に内接する四面体に関する問題です。
(1)MがT3T4の中点であることを利用すると、(ii)の式からT1T2の中点Nは、直線OM上にあって、なおかつOがMNをk:1に内分する点だと分かります。
よって、底辺をT1T2,高さをMNとすれば面積が計算できますね。
(2)四面体の体積を、(1)で考えた三角形を底面とする2つの三角錐の合計と解釈出来れば考えやすくなります。
T1T2を固定した状態でT3T4を回転させていくと、ちょうどこの2線分が垂直になった時にこそ体積が最大になることが分かります。
こうしてV(k)が計算でき、実質3次関数の増減の問題に帰着できます。kで微分して増減を調べましょう。
<筆者の回答>

第3問

整数問題です。
(1)(2)ともに、題意を満たすようなnを一般的に求め、100番目の数を調べる、という流れになります。
(1) nを7で割った余りで分類し場合分けすればよいでしょう。
(2) 91=7×13なので、n^2+n+1が「7で割り切れ」かつ「13で割り切れる」ようなnの条件を調べればよいことになります。
7で割り切れる条件は(1)で調べているので、それを満たしたうえでさらに13で割り切れる条件を考えていきます。ということで、(1)と同様に13で割った余りで分類し場合分けしましょう。計算はかなり面倒ですが・・・
<筆者の回答>

