2024年も大学入試のシーズンがやってきました。
今回は、東北大学の理系数学に挑戦します。
<概略> (カッコ内は解くのにかかった時間)
1. 2次関数に関する面積(25分)
2. logに関する不等式評価(60分)
3. 確率漸化式(35分)
4. 2つの球の交線(60分)
5. logのグラフと関連する整数問題(40分)
6. 円錐側面の面積(75分)
計295分
<体感難易度>
1<3<5<4<6<2
個人的には東北大史上最凶のセットでは?と思うくらいに激難なセットです。
全体として、細かい小問で部分点を拾い集めることはできても完答するのは至難な問題が多い印象です。
第1問は2次関数の問題で今回のセットでは最も易しい問題です。正直この問題を落とすと完全に後がなくなるので確実に完答したいです。
第2問は(1)の不等式評価が「理系出題」であるがゆえに却って難しくなっています。文系であればまだ手が付けられたかもしれません(詳しくは後述)なお(2)は(1)とは独立に解けるので、(2)だけ解いて部分点を稼ぐのが有効です。
第3問は確率漸化式の問題で、(4)をどう考えるかが分水嶺です。
第4問は球の交線となる円に関する問題で、(3)までは何とかなっても(4)が難しいです。
第5問も(3)まではスムーズにいけますが、それを利用する(4)が意外と面倒です。
第6問は曲面の面積ということで誘導は付いてるもののかなり難しいです。
<個別解説>
第1問

2次関数に関する面積の問題で、この問題は全体の難易度を考えると絶対に落とせません。
(1)Aの座標からpを求め、接線の情報からqを求めるという一本道の問題です。
(3) (2)ができていればボーナス問題です。
<筆者の解答>
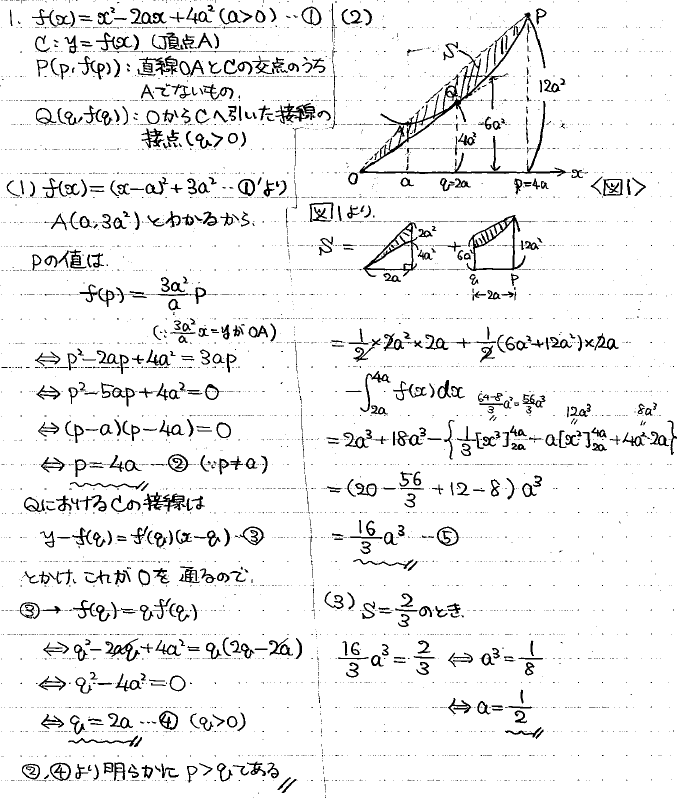
第2問

logに関する不等式評価の問題です。
(2)は難しくないのですが、(1)がとにかく難しく筆者自身大苦戦しました。
(1)一見するとよくある不等式の問題ですが、与えられているxの条件がどちらも奇怪なものでどう取り扱えばいいのか、いまいちよく分かりません。
理系の受験生であれば、示すべき不等式を見た瞬間に「左辺ー右辺をxの関数と見なして微分して、増減を調べるんだな!」と発想するはずです。実際私もそうしました。でも、今回の問題、その方法だとうまくいかないのです。
(a)(b)を、とりあえずtを固定したxの条件に焼き直して上の方針で取り組もうとしましたが、極小値の符号判定がカオスの極みになったりと全くうまくいきませんでした。それ以前に(b)はxをtの式でうまく表現できない形の不等式です。
ここでとても意地悪な点が一つあります。実はこの問題、文系との共通問題なんです。文系用の問題として出題されていれば、そもそもlogの微分を知らないので「左辺ー右辺をxの関数と見なして微分する」という発想が出て来ません。なので、最初から微分以外の方法で攻めようと考えるはずなのです。
でも受験本番では「この問題は実は文理共通」なんて知る由のない理系受験生の多くが、微分する方針で突っ走り撃沈させられるわけです。気の毒としか言いようがありません。
というわけで、正解ルートを紹介します。
実は、(a)の不等式を単純に等価変形することで右辺の形ができ、左辺も(b)を使うことで出現させられます。これでお終いです。
言われてみれば「な~んだ」ってなる解法ですが、これを試験中に思いつけた理系受験生がどれだけいたか。
そもそも微分する発想すらないがゆえに最初から式変形でなんとかしようと発想できる文系受験生の方が正解ルートにたどり着きやすく、逆に下手にlogの微分を知ってるばかりにテンプレ解法に流れやすい理系受験生の方が苦戦する、そんな意地悪な問題でした。
そして続く(2)は(1)を全く使わずに解けてしまうというのがより悪質度を高めています。
(2)繰り返しますが、(2)は(1)とは全く独立に解けてしまう問題です。下手に(1)があるばかりに無理に(1)を使おうとして思考を歪まされた受験生も多そうな気がします。
さて、(2)は単品で見ればよく見る問題です。
与式を式変形すると2^n≦n^2となるので、こうなるnを求めればいいわけです。
基本的には指数関数の方が2次関数よりも大きくなるので、こうなるnはレアケースだと想像できます。実際に実験してみるとnは2,3,4の3つしかなさそうです。
あとは、n≧5の時にこの不等式が成り立たないことを帰納法で示せばお終いです。
<筆者の解答>

第3問

確率漸化式の問題です。
(1)n=2の場合はそれぞれ、AA,BA,ABとなる場合なので計算は容易です。
末尾にどの文字なら来て良いかを考えると漸化式が作れます。
(2)(3)
問題文に従ってpn+2qn+2rnを計算すると等比数列の形の漸化式が出来ます。(3)についても同様です。
(4) (3)までで求まった一般項だけではpn=rnが上手く処理できません。もう1本(2)(3)と似たような形の漸化式・一般項が欲しくなります。とはいっても、(2)にしても(3)にしてもかなり出来過ぎた線形和だったので、そんなものが1から新たに作れるか、という話になります。
しかし、実は超お手軽にもう1本の式を調達できます。(3)の数列は虚数でした。虚数と言えば「複素共役」・・・そうです。(3)の結果全体に複素共役をとれば、もう1本の式ができませんか?j実はこれでうまくいきます。
複素共役同士の一般項でqnを消してあげれば、見事にpn-rnの一般項が求まるので、あとはその値が0になるようなnを探してあげればよくなります。
複素数の方程式なので、極形式に直してド・モアブルの定理を使うのが定石です。
問題の解説はこれで終わりなのですが、(2)(3)で考えた数列の係数は、大学1年で学ぶ線形代数の知識があると1から自分で求めることができます。その背景があるからこそ私は「複素共役をとればもう1本式を作れる」という発想をすぐに思いつけたわけです。参考までに、その背景部分も添付しておきます。
<筆者の解答>


↓以下参考情報として、なぜ(2)(3)の数列が上手く等比数列になってるのかの背景となる計算を載せておきます。簡単に言うと、線形代数における「対角化」の作業を行うことで必然的に出てくる数列なのです。大学1年の終わり、行列の対角化を学んだあとに個々の計算を覗くと理解が深まるのではと思います。



第4問

2つの球の交線となる円に関する問題です。
(1)距離を計算するだけであり、説明不要ですね。
(2)球の中心間距離が、「半径の差より大きく、半径の和より小さい」ときに2つの球は交線を持ちます。
残りの部分は、三平方の定理やベクトルの知識を駆使することで求まります。
(3)求めるベクトルをpとすると、pはxy平面と平行な単位ベクトルなのでp=(cosθ,sinθ,0)と置くことができます。
Hに平行なベクトルを直接考えることは難しいので、Hの法線ベクトルを準備して、その法線ベクトルとpが垂直になる条件を処理したほうが楽です。Hの法線ベクトルはP1P2ベクトルそのものですね。
ここまでは何とか本番でも解き切りたいところです。
(4)最終的にOQを最小化したいので、C上の点Qの座標をうまくパラメータ表示したいところです。
CはP3を中心とする円なので、まずは始点をP3として考えるとよいでしょう。
ここで、H内にある単位ベクトルの1つには、(3)で求めたものがありました。(3)で求めた2本のうちの1本の単位ベクトルをaとします。
このとき、H内にありつつもaとは一次独立な単位ベクトルbがあれば、H上の点Qは、P3Qベクトル=sa+tb (s,tは実数)で網羅できるんでした。
しかしどうせこの形にするならbをもっとうまく選びたいですよね、例えばa・b=0となるような。
要するに、H内にあってaと垂直な単位ベクトルをbにしてしまえば、普段使ってるxy座標と同じ感覚で係数s,tを取り扱えるようになるのです。
CはP3中心の半径1の円なのだから、s=cosφ,t=sinφとしてしまえば、QがC上の点として網羅した形にできます。
ここまでお膳立てができれば、あとはOQが最小になるようなφを決めてあげればよいだけになります。
[訂正] ベクトル計算にミスがあったこと、そして求めるものはOQではなくQとxy平面との距離でした。その2点を勘違いしたまま回答していたため、訂正いたします。
<筆者の解答>


第5問

logのグラフと関連する整数問題です。
(1)f(x)を微分を計算するだけです。
(2)g(x)を微分することでg(x)の増減を調べられます。g(x)<0となるxは、logの中身がeのべき乗になるように探すと見通しが良くなると思います。
(3) (2)の結果からx=αを境にf(x)は増加→減少に転じることが分かり、問題文のヒントからx→∞の極限もわかるので、グラフが書けることになります。
(4)与式を変形すると、f(m)=f(n)となるので、y=f(x)のグラフとx軸平行な直線との交点x座標がmとnということになります。
グラフの形から2<m<αにmの値を制限できるのですが、詳細を詰めるにはαの値を評価しないといけません。
とはいえ、分かりやすい整数値をf(x)に代入する形だと3<α<6までしか絞り切れないので、これ以上の深堀は諦めてmは3,4,5のどれかだと絞って個別検討に入ってしまいましょう。
第2問(2)でも述べましたが、基本的には指数関数の方が2次関数よりも強いためnを下から順に代入して等しくなるケースを探して、等しくなくなったnの値以上ではもう等しくなることはないことを言えばOKです。
(第2問(2)でやったような帰納法を使うことで証明可能ですが、今回は面倒なので示せる旨だけ記述して終わりにしています。)
<筆者の解答>


第6問

円錐側面の面積に関する問題です。誘導が付いてるとはいえ、曲面の面積という慣れない題材故に解きにくいでしょう。
(1)Kの側面をx,y,zの方程式で表現することで、E上の点Rをパラメータ表示できます。このRがPQ上にあることから別の形でパラメータ表示できるので、2つの表示が一致する条件からRの座標が求まります。
(2)円錐側面の展開図を考えると考えやすくなります。側面の展開図の中心角と底面の展開図の中心角の関係は、両者の弧の長さが等しいことから求まります。
こうすることでS(θ+h)-S(θ)は、中心角h/√2の半径r(θ)の扇形よりは大きく、同じ中心角の半径r(θ+h)の扇形よりは小さい、と評価できることになります。それを立式すれば与式となります。
(3)hを限りなく小さくしてS(θ+h)-S(θ)を-π/2≦θ≦π/2の範囲で足し合わせれば、円錐の上側の側面積になります。つまり、(2)の不等式をhで割ってh→0の極限を取ればS'(θ)が求まり、S'(θ)を上の範囲で積分すればよくなります。
この積分の過程でヒントの置換を行うとうまく積分計算が進みます。
これで求まるのはあくまで側面の上側なので、お目当ての下側の面積は、側面のx>0の部分全体から求めた上側の面積を引けばよいわけです。このとき、側面の展開図の中心角に注意が必要です。
<筆者の解答>


