旧帝大の文系向けの過去問を取り上げます。理系との共通問題は理系の記事を参照して頂くこととし、基本は文系ユニークの問題のみ取り上げます。
この記事では東北大学の1996年の問題を取り上げます。
理系の記事はこちら↓
平成の東北大理系数学 -1996年- - ちょぴん先生の数学部屋 (hatenablog.com)
第1問

直線と楕円の交点に関する問題です。この時代では、2次曲線も文系の範囲内だったようですね。
今回はy座標に関する情報が与えられているので、xを消去してyの「2次方程式が2つの正の実数解を持つ条件」を求めればOKです。が、そのためには直線の式をx=の形にしたいので、a=0だと具合が悪いです。よって、a=0の場合だけ例外扱いで処理する必要があります。
<筆者の回答>
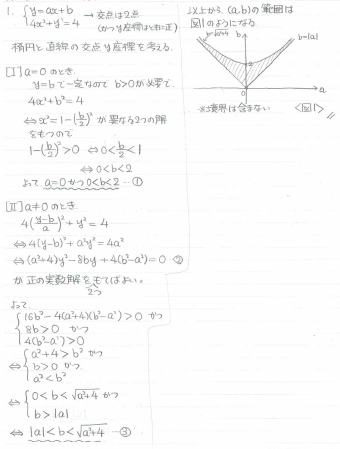
第2問

ベクトルの和を計算する問題です。
(1) pnは、p1を(n-1)θ回転したベクトルなので、cos,sinで成分表示できます。
(2) ベクトルの各成分が、等比数列とcos,sinの混じった式になるので、各成分でΣ計算するのは大変です。ここは複素数の知識を使うと楽になります。
z=α(cosθ+isinθ) と置くと、pnのx座標はz^(n-1)の実部、y座標はz^(n-1)の虚部になるので、各成分の和を計算する代わりにz^kの和を計算してあげれば、その和の実部が求めるx座標、虚部がy座標となります。そして、z^kの和はただの等比数列の和なので計算が楽です。
<筆者の回答>

第3問

空間図形の問題です。
この問題は、球の中心とA, Pを通る平面で切断して平面の問題に帰着させると楽です。座標を使わずとも相似の関係を使えばAの座標、rの値が求まります。平面αの式は、法線ベクトルがAPベクトルになることを利用すれば求まります。
<筆者の回答>

第4問

3次関数の極値と面積に関する問題です。
(1) f'(a)=0を利用すればOKです。ちなみに、この関係式だけだと極小値の可能性も排除できていませんが、もう一つの極値を調べてあげればちゃんとf(a)が極大値になっていることが分かります。
(2) y=f(x)とy=f(a)の交点を求めて積分を計算する基本問題です。
<筆者の回答>
