このシリーズでは、平成の京大理系数学の後期入試の問題を1年ずつ遡って解いていきます。
2006年を最後に後期入試が廃止されたので、初回は2006年になります。
第1問

恒等式に関する問題です。
とにもかくにもA(x), B(x), C(x)を全て文字式でおいて、恒等式となる条件を求めてあげるのが先決でしょう。ここでは係数比較で十分でしょう。
文字数を減らすために、C(x)の定数項が0か否かで場合分けして検討を進めるとよいでしょう。さらに単位円の式が登場するので、三角関数で変換するのは自然と思いつくでしょう。(※答案の⑤’式の左辺をベクトルの内積と見なして、大きさ1の2つのベクトルの内積が1なら両者は同じ向きを向いていないといけない、と図形的に解釈してもOKです)
<筆者の解答>

第2問
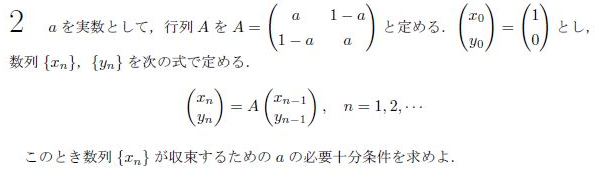
連立2項間漸化式に関する問題です。
xn, ynの一般項を出すために、与えられた漸化式を足し引きして等比数列が作れないかを考えるとよいです。
幸い今回の問題では単純な足し算と引き算だけで作れてしまいますが、答案ではより汎用性の高い xn +αyn = β(xn-1 +αyn-1) となるα,βの組を愚直に求める方法を取っています。
一般項が求まりさえすれば、後は公比が-1より大きく1以下なら収束することが分かるのでそうなるaの条件を求めに行きます。
<筆者の解答>

第3問
![]()
確率の問題です。
実験をしてみると分かりますが、n個のサイコロの目の和がn+3になるパターンは殆どない事に気が付きます。なにせ「1」がn個並んだだけで和がnになるので、余った+3をどう振り分けるかでしかパターンが生じません。
パターンが絞り込めれば、それぞれの確率を計算して足し上げるだけです。
<筆者の解答>

第4問

三角形の内接円半径を評価する問題で、正直このセットでは一番難しい問題だと思います。
内接円半径rを計算するには、△ABCの面積Sと、外周の長さLの情報が必要です(この2つがあれば、r=2S/Lで求まります)。そのためには座標を設定しないとどうにもならなさそうです。Oについて回転対称性があるので、C(1,0)としても一般性を失いません。
その下でA(cosα, sinα), B(cosβ, sinβ)とおいて、SとL、ひいてはrをα,βの式で表しに行きます。
式変形を進めると、rは、3つの正の数の(積÷和)という比較的綺麗な形で書けることが分かります。(分子は半角の形にした方が明らかに見通しがよいです)
さて、問題はここからです。
α、βという2文字が分数の形で登場していて、かつ分子と分母の両方に登場している厄介な形をしています。このまま微分で攻めるのは厳しそうです。
ここで、問題文をよく読むと「rは1/2以下であることを示せ」となっています。「rの最大値が1/2であることを証明せよ」とは書かれていないことに注目すべきです。
rの最大値を計算するわけではなく、「とにかくrが1/2以下って言えれば何でもいい」って開き直ることができるわけです。ということは、rをガバガバでもいいのでとにかく上から押さえこんでいけばよいのでは?っていう考えに至ります。
だから、rの式その物の最大値を調べる必要はなく、rよりも大きい「より最大値を調べやすい式」を使って押さえればよいということになります。
ということで、3つの数の対称式(それも和と積のストレートな形)になっているから、3変数に対する「相加相乗平均の関係」を使えばよさそうです。これに気付けたかが大きなキーポイントです。
そうすることで、最大値を調べる関数を遥かに簡単な形にすることができます。
あとはお馴染みの予選決勝法で愚直に攻めて最大値を計算しにいきましょう。結果として無事、rが1/2以下であることが示せます。
ちなみにr=1/2となるのは、結果から分かる通り△ABCが正三角形になるときですね。
<筆者の解答>


第5問

微分方程式の問題です。
この問題、実は以前の記事、
ガクエンワルドを倒すために必要な難問たち ~機界戦隊ゼンカイジャー 第33カイより~ - ちょぴん先生の数学部屋
で解説済みの問題になります。ゼンカイジャーの33話に登場した上から2番目の数学の問題です。なので、詳しくは上記の記事をご覧ください。
<筆者の解答>

第6問
![]()
入試史上「最も問題文が短い」問題としてかなり有名な問題ですね。
tan1°が有理数か無理数かを判定せよ、というのがこの問題の趣旨となります。
最初の分かれ道は、どっちだと決め打って検証するかです。
仮に有理数だと思ってそれを証明しようとすると、原理的にはtan1°の具体的な式を計算すればよいのですが、どの有名角からも簡単に計算できそうにありません。
というか、直感的にどう見ても「無理数」っぽいですよね笑、tan1°って。無理数であることを示すには、「有理数だと仮定して矛盾を示す」という、いわゆる背理法のテクニックが使えます。
加法定理などの道具立てもあって見通しが良いので、もう「無理数だ」と決め打って証明しに行った方がよさそうです。
tanの加法定理がtanを使った分数の式になるので、tan1°が有理数ならtan2°も有理数、tan3°もtan4°も以降のtan(整数)°も全部有理数になっているはずです。
ところが、我々がよく知っているtan30°の値は1/√3であり、明らかに無理数です(さすがにこれは自明扱いしていいかと)。これで矛盾が示せました。
別解として倍角の公式を使うパターンも紹介していますが、本質的には同じようなものです。
<筆者の解答>
