このシリーズでは、東京医科歯科大学の数学の問題を解いていきます。
25回目の今回は1998年です。
第1問

円の存在領域を考える問題です。
(1) 考えやすくなるように、Eを原点において、長方形の辺が軸平行になるように座標設定するとよいです。
円の中心を極座標で表現して、円が長方形の中に入るようなr,θの条件を考えていきます。今回は面積を調べたいので、円が長方形に内接する条件だけ考えればOKです。
積分計算は、t=tanθ/2の置換でうまくいくタイプです。
(2)考え方は(1)と同様で、今回も面積を計算したいので「円がHを通って、なおかつFに内接する場合」に絞ってPの領域の境界線を調べてあげます。
積分計算は(1)同様t=tanθ/2の置換で進めますが、高校数学の範囲ではもう一段解置換する必要があります。
なお、この積分計算は、大学数学で習う「留数定理」という裏技を使うと、置換方法を思いつくことなく機械的に計算できてしまいます(別解にて紹介)。
この留数定理については本ブログでも軽めに紹介していますが、
虚数の力で積分が解ける! ~コーシーの積分定理・留数定理~ - ちょぴん先生の数学部屋 (hatenablog.com)
ちょうど、ヨビノリさんが詳細な動画を上げていましたので、興味のある方はぜひご覧ください。
<筆者の解答>
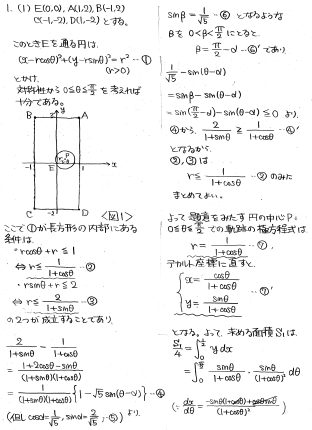


(2)の積分を留数定理で解く別解です。

参考
※(1)でのPの存在領域の境界線(第1象限)

※(2)でのPの存在領域の境界線(y≧0)

第2問

確率の問題です。
n+0.1秒後という表現が見慣れないですが、この問題の設定の都合上「粒子が合体して動き始めた直後」くらいの意味合いです。
(1)k=1の場合は全ての粒子がDに移動するとき、k=3の場合は全ての粒子がバラバラな頂点に移動するときです。k=2の場合は直接数えにくいので余事象を利用するとよいでしょう。
(2)n-1秒後まではk=3が続いて、その直後の移動によってk=2になる確率を考えればよく、(1)の結果を利用しましょう。
(3) k=2の状態からk=2のままになる確率、k=1になる確率を新たに考えることになります。
P2(n)については、l秒後にk=2になってそれを維持する確率の和なので(2)のQ(n)が利用できます。
P1(n)については、k=3から直接k=1になる場合と、k=3がk=2を経由してk=1になる場合が混在して直接計算しにくいので、余事象を利用します。(※P3(n)は容易に計算できます)
<筆者の解答>
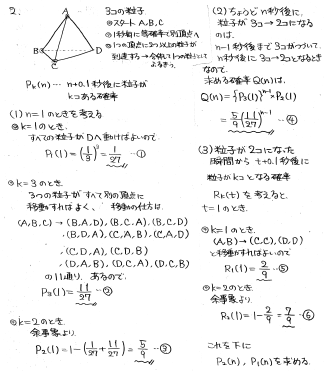

第3問

(1) 1/(t+1)がlog(t+1)の微分だと気付ければ、置換積分で片が付きます。
(2) (1)から結果が予想できるので、帰納法で証明です。
(3) SnとSn+1の漸化式を求めることになるので、Sn+1をSnで表すことを目標にしていきます。すると与式の右辺の分子に等比数列が現れるので、その公比が1になるようにaを決めてあげればOKです。
(4) (3)の両辺に(-1)^(n+1)をかけてあげると階差数列の形にでき、そこから与式の形が導けます。あとはn→∞での極限を考えてあげればよいわけですが、Sn→0を示す必要があります。
なお、この(4)の結果は、e^xのテイラー展開の式にx=-1を代入することで即座に求めることができます。
<筆者の解答>

