先日行われた2023年度の九州大学の後期数学を解いてみました。
第1問

(筆者注:(3)は囲む曲線としてy=e^bxを追加してください。書き写すときに漏らしてしまってすみません。解答ではこの曲線も反映していますので、影響はありません)
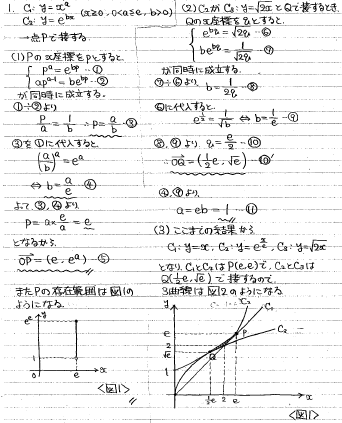
互いに接する曲線に関する問題です。
(1)(2) 接点でのyの値と微分係数が両方一致する条件からa,b, Pのx座標、Qのx座標が全て求まります。
(3)図を丁寧に描くことで、積分計算で面積が計算できます。
<筆者の解答>

第2問

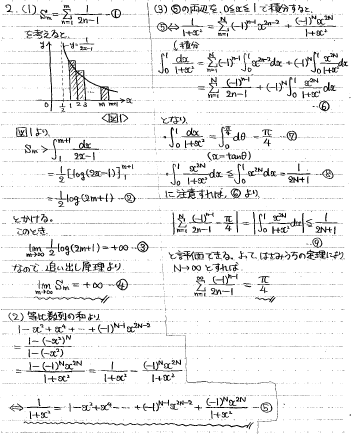
無限級数の収束発散を調べる問題です。
(1)面積を使うと、Σがn→∞で発散する関数で下から押さえられるので、追い出しの原理から発散が証明できます。
(2)等比数列の和の公式を利用すれば容易に証明できます。
(3) (2)の式を利用して考えていきます。
xの指数の肩が2n-2なことと、最終的に2n-1を分母に持っていきたい、という発想から、「(2)を積分すればよさそう」と思いつきます。積分範囲は、余計な指数関数が生まれないように0≦x≦1とすればよさげです。
そうすると、(2)の右辺の和の部分が調べたい級数になり、左辺はx=tanθの置換からπ/4と計算できます。残すは右辺の最後の積分だけです。
この積分は直接計算は厳しいですが、不等式評価はできます。Nの式で評価したいので、Nが関係しない分母1+x^2を定数に変えて積分の外に追い出せばいいですね。
これで、はさみうちによって右辺の最後の積分はN→∞で0に収束することが分かりますので、両辺で極限を取れば、お目当ての無限級数はπ/4に収束することが分かります。
余談ですが、このライプニッツ級数は、それ自体は収束するものの各項で絶対値を取ってから和を取ったもの(要するに(1)の級数)は発散するという性質を持っていて、この性質は「条件収束」と呼ばれます。条件収束する無限級数は、足し算の順番を変えると答えが変わってしまうことが知られています。
(このあたりの話は、この記事で取り上げています。「無限」には常識が通じない その1 ~足し算の順番を変えると答えが変わる?~ - ちょぴん先生の数学部屋 (hatenablog.com) )
<筆者の解答>
第3問

確率の問題です。
(1) 和が5になるような出方を全て列挙すればお終いです。但し、目の順番もちゃんと考慮する必要があることに注意です。
(2)直接場合の数を調べても解けますし、「最小値が4→『4~6しかでない』-『5~6しかでない』」という考え方から解くこともできます。
(3)奇しくも北大後期でほぼ同様の問題が出題されていました。
基本的には「~で割り切れない」という余事象で考え、ベン図を使って計算すると見通しが良いです。
(4)要するにb^2 -4ac=0となるような(a,b,c)の組み合わせを列挙すればよいわけです。
<筆者の解答>


第4問

三角形に関する問題です。
全体として各小問の繋がりが希薄で計算が面倒な、本セット最難問と言えると思います。
最初に、∠ACB=90°と|AB|=2|AC|をa~dを使って言い換えておきましょう。
(1)内積を使うと、実質c-a, dの2つの量がa,bで書ければcosθ、sinθをa,bだけの式で書けることになります。が、この2つの計算がかなり面倒です。
冒頭の2つの条件式を連立していくのですが、まずはcの部分をc-aの塊にして考えると見通しが良くなります。とはいえ、そこからも連立の仕方を工夫しないと解き進められません。
結果、2通りの解が求まりますが、Cが第1象限にあるという条件から1択に絞れます。
このことは、図を描いてみると理解できます。
冒頭の2条件を考えると、円周角の定理からCはO,A,Bを通る円周上にあって、なおかつ△ABCは1:2:√3のタイプの直角三角形になります。この状況を図にすると、Cは第1象限か第4象限にしか存在できないことが視覚的に分かります。
(この図を使えばもっと簡単にsinθ, cosθを調べられそうなので、そこは反省点ですね・・・)
[追記] 図を使った別解を追加しました。こちらはtanの加法定理を使えばいいので遥かに楽に解けましたね。。。
(2)△ABCの内心をIとしたときにOIベクトルをOA, OB, OCベクトルで表現することを目標にします。角の2等分線の性質からメネラウスの定理を使うことでこのベクトル表示が導出可能です。
(3)△OABの内心をJとすると、(2)と同じようにOJベクトルを調べられます。このときs=IJなので、内積を利用してsを計算していけます。が、最終結果は2重根号もある複雑な形になるのでかなり不安になります。
AB=lはa^2+b^2=l^2と言い換えられ、これはab平面における円になっています。この下でsを考えると、k=(2-√3)a+bが最大になるときsが最小になり、この式はab平面上の直線になるので、結局線形計画法の問題に帰着できます。
<筆者の解答>




(1)の別解です。

第5問

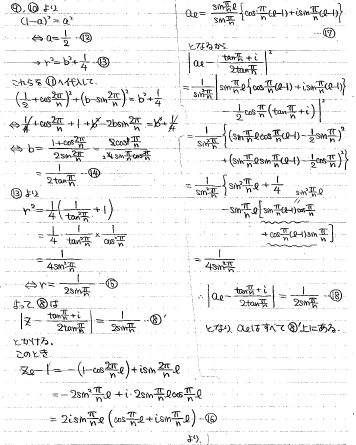
複素数平面の問題です。
(1)zk = z1^kと言い換えられるので、そこから等比数列の和の話に持っていけます。
(2)三角形の辺の長さとなす角のsinが調べられれば面積が計算できます。
(3)いきなりn角形の外接円と言われてもピンとこないので、まずはP1~Pnから分かりやすい数点を選んで、その数点の外接円の式を調べ、最終的に残りの点もこの円周上にあることを確かめる、という流れで考えるとよいです。
最初に選ぶ点ですが、まずl=1の場合はa1=1で分かりやすいですね。次にl=nの場合もan=0と分かりやすい点になります。円が固定されるにはあと1点必要なのですが、それはl=2としたときのa1=z1+1を採用すればいいでしょう。
あとは上記の流れで解けばよいのですが、とにかく計算が煩雑です。2倍角の公式を使って各度を2π/nからπ/nに変えておくと式が多少はスッキリします。
面積については、(2)の知見からこのn角形が各辺の長さが1の正n角形になっていることに注目して、n等分してできる三角形の面積を調べてn倍にする、という考え方で調べられます。
<筆者の解答>