皆さん、こんにちは。
今回は、「正多面体は5種類しかない」ことを証明してみたいと思います。
1. 正多面体とは?
正多面体とは、以下の3つの条件をすべて満たす立体のことです。
条件1: 全ての面が合同な正n角形である。
条件2: 凸多面体である(凹みがない)
条件3: 全ての頂点について、そこに集まる辺や面の数が等しい
特にこの条件3の存在によって、非常に対称性の高い立体となっています。
そんな正多面体ですが、以下のような5種類のものが知られています。
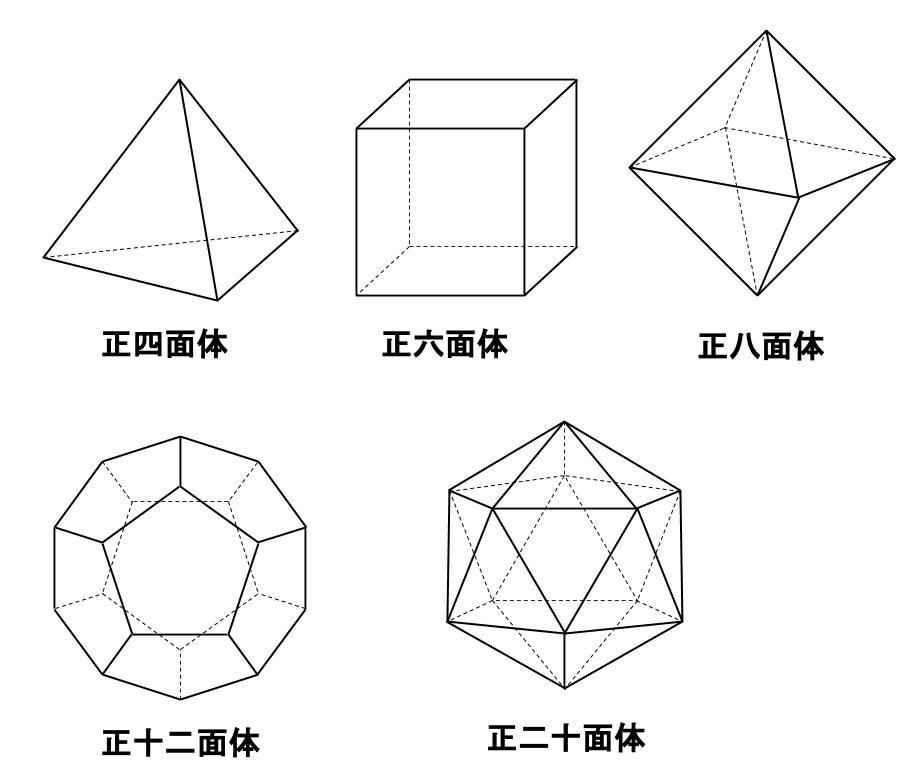
※参照元【中学数学】正多面体 | 中学数学の無料オンライン学習サイトchu-su- (komaro.net)
そして、正多面体は上記の5種類しか存在しません。これはまだ発見されてないわけではなく、「6個目以降は存在しないこと」が証明されています。
今回のメインテーマは、この『6個目以降は存在しないことの証明』の紹介になります。
2. オイラーの多面体定理
正多面体が5種類しか存在しないことを証明するための道具立てとして、先に「オイラーの多面体定理」というものを証明します。
オイラーの多面体定理は、立体の「頂点」「辺」「面」の各々の個数の間に成り立つ関係式で、次のようなものになります。

(ちなみに、VはVertex(頂点)の、EはEdge(辺)の、FはFace(面)の頭文字です)
現実のいくつかの立体を考えると、確かに成立してることが分かります。

このオイラーの多面体定理を順を追って示していきます。
2-1. 閉じた面のない平面グラフ=「木」
電車の路線図のように、「頂点」を「辺」で繋いでできる図形のことを「グラフ」と呼びます。オイラーの多面体定理は、この「グラフ」について研究する学問「グラフ理論」についての定理となります。
最初に、閉じたループがないグラフ(=木)について考察してみましょう。

この木については、
「最初に1つの頂点●を作る」→「ー●を次々に追加していく」
というプロセスでどんな図形でも作れてしまいます。追加される頂点と辺の個数は常に1つずつなので、
「頂点の個数」ー「辺の個数」
はどんなにー●を追加しても変わらないはずです。スタートが「頂点=1個、辺=0個」なわけですから、結局

が常に成り立ちます。
2-2. 閉じた面のある平面グラフ
次に、木に「閉じたループ」を作ってみます。以下、辺で囲まれてできる閉じたループを「面」と呼ぶことにします。

木にある2つの頂点の間を1つの辺で繋いであげると、面が1つ誕生します。
辺を1個追加すると面が1個誕生するので、

が成立します。よって、①にこれを適用してあげると、

となります。面の数=0とすれば①に戻る(木に戻る)だけなので、結局③は①の拡張になっています。
2-3. 3次元空間上にある木
今度は、木を3次元に拡張してみます。具体的には、わかりやすく球面に先の木を張り付けてしまいましょう。

この球面を平面に展開すると、元の木に加えて「球面だった『面』」が追加されることになるので、①に面の情報を足すことで

が得られます。
2-4. 3次元空間上にある、閉じた面を持ったグラフ
同様に、球面に張り付いた、「閉じた面を持ったグラフ」を張り付けてみます。

ここでは、球面上に4点を取って、それを正四面体のように球面上にある辺で繋いだグラフを考えることにします。
さて、ここで、面のうちの一つを取っ払って穴を開けてしまいます。そして、その穴から空気を吸い込んで球面を萎ませていきます。すると、最終的には、頂点と辺が全て同一平面上に収まります。
この最終形は、2-2の「面を持つ平面グラフ」そのものなので、③がそのまま成り立っているはずです。
そして、本当はこれに「最初に取っ払った面」1つが加わっているはずなので、結局

となります。2-3と全く同じ式ですね。
上記は丸まった「正四面体もどき」での議論でしたが、辺が真っすぐな正四面体でも全く同じ議論になるため、結局これで「オイラーの多面体定理」が証明できたことになります。
3. 正多面体が5種類しかないことの証明
では、いよいよお目当ての「正多面体が5種類しかない」の証明を行います。
今回の問題は、入試風の文章に直すと次のようになります。

結局、正何角形を、1つの頂点に何枚集まるようにして、合計何枚使えば正多面体を作れるか?という問いを、オイラーの多面体定理を使って整数問題に帰着させるのが目標です。
オイラーの多面体定理に倣って、正多面体の頂点の数をV, 辺の数をE, 面の数をFとして、V,E,Fをl,m,nの式で表現してオイラーの多面体定理の式に代入する、という方針で考えましょう。
(※nが3以上なのは当たり前で、1つの点に2枚以下しか面が集まらないとそもそも立体が作れないのでmも3以上、そして面が2つ以下だとやはり立体が作れないのでlも3以上で確定です)
3-1. V,E,Fをl,m,nの式で表現
まず、面の数Fについては簡単です。問題文で正n角形をl枚使うと指定されてるのですから、

に決まってます。これはよいでしょう。
次に、頂点の数Vについて考えます。
例えば、正四面体は4枚の正三角形を使って作れるわけですが、そうすると頂点の個数を3枚分ダブルカウントしてしまってますね。

一般化すると、元の正n角形l枚の頂点のうち、1つずつ合計m個の頂点が合体して1つの頂点になるわけです。
よって、1つの頂点につきm回分のダブルカウントが生じてしまうので、元々の頂点の総数n×l個をmで割ってしまえばVが求まります。

最後に、辺の数Eについて考えます。
これも正四面体の例で考えます。
正四面体の各辺を中点で切断して4つの部分に分けると、1つの頂点に半辺3つが生えた図形が出来上がります。

一般化すると、1つの頂点に半辺m個が生えた図形が出来上がり、頂点自体の総数がV個、半辺を2つ繋げると1つの辺になることに注意すれば、Eは

と計算できます。
これで、V,E,Fのすべてがl,m,nの式で表現できたことになります。
3-2. オイラーの多面体定理の式に代入
以上を、オイラーの多面体定理の式に代入して整理すると、

という式が出来上がります。
この式、実は大学入試の過去問で出題されたことがあります。阪大の2010年理系第3問です。

平成の阪大理系数学 -2010年- - ちょぴん先生の数学部屋 (hatenablog.com)
阪大の問題では、いきなりこの関係式を解けとなっていましたが、実はこの通りオイラーの多面体定理を表現する式だったのです。
ということで、あとはこの阪大の問題を解けばよいことになるので、以降の解説は上記解説記事に任せることにします。
いずれにせよ、この式を解くことで、(l,m,n)の組が次の5種類しかないことが分かります。

左から、正四面体、正六面体(=立方体)、正八面体、正十二面体、正二十面体、に対応しています。
これで、正多面体が以上の5種類しかないことが証明できました。
(おまけ)別解
実は、オイラーの多面体定理を使わずに証明する方法があります。
それは、「1つの頂点にm枚の正n角形の面が集まる時、その内角の和は360°未満じゃないといけない」という条件から必要条件を導く方法です。

ここからも同様に(m,n)の組が5種類しか出てこないため証明できたことになります。
ただ、この方法だと実際に多面体を作れるという十分条件が見切れておらず、さらに面の個数がすぐには分からないので、全ての情報が必要十分に導出できるオイラーの多面体定理を使う証明の方が格上だと私は感じます。